A theorem is a mathematical statement that has been proven using known facts. The Pythagorean Theorem is one of the most widely known and used theorems. It derives its names from a Greek philosopher and mathematician named Pythagoras of Samos (570-495 BC), who was credited with being the first person to prove this theorem.
The Pythagorean Theorem is a mathematical statement about the relationship between the sides of a right triangle. A right triangle is a triangle in which two of the three sides meet to form a 90-degree angle. In a right triangle, two of the sides are called legs, and one side is the hypotenuse.
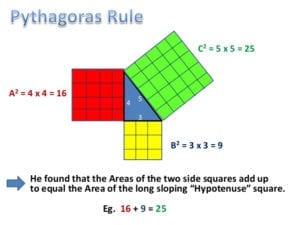
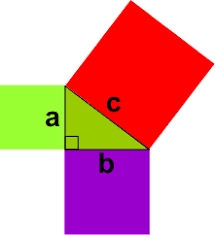
Over 2000 years ago, an amazing discovery was made about triangles: When a triangle has a right angle (90 degrees) and squares are made on each of the three sides, the biggest square has the same area as the other two squares put together. See figure 1.
This is called the Pythagorean or Pythagoras’ Theorem and can be written as an algebraic equation: a2+b2=c2, where c is the longest side (hypotenuse), a and b are the other two sides (legs). The formal definition of this mathematical statement is: the square of the hypotenuse is equal to the sum of the squares of the sides in a right triangle. See figure 2
If we know the lengths of two sides of a right triangle, we can find the length of the third side. Again, the formula is a2+b2+c2. We are going to solve for c(hypotenuse):52+122+c2=25+144=c2 which equals25=144=c2, swapping sides, we now have c2 =169 and c=√169=c=13.
We may solve for any side: we will start with the basic equation: a2+b2=c2. We will solve for a leg of the triangle instead of the hypotenuse. 92+b2=152=81+b2=225, transposing the formula we now have b2=225-81-b2=144, taking the square root of both sides we now have b=√144, b=12
Real Life Uses of the Pythagorean Theorem
Architecture and construction: Given two straight lines, the Pythagorean Theorem allows you to calculate the length of the diagonal connecting them. For instance, if you are building a sloped roof and you have the height and length of the roof, you can find the diagonal length of the roof’s slope. You can use this to properly cut the joists for the roof, or calculate the area of the roof you would need to shingle.
The Pythagorean Theorem is also used in construction to make sure buildings are square. When laying out a foundation, or constructing a square corner between two walls, workers will set out a triangle from three strings that correspond to these lengths. If the string is measured correctly, the corner opposite the triangles’ hypotenuse will be a right angle, so the builders will know they are constructing their walls or foundations on the right lines.
Navigation
The Pythagorean Theorem is also useful for two-dimensional navigation. For instance, if you are at sea and navigating to a point 300 miles north and 400 miles west, you can use the theorem to find the distance from your ship to that point and calculate how many degrees west of north you will need to follow to reach that point. The distance north and west will be the two legs of the triangle, and the shortest line connecting them will be the diagonal (hypotenuse).
The same principle can be used for air navigation. A plane can use its height above the ground (altitude) and its distance from the destination airport to find the correct place to begin a descent to that airport.
Surveying
Surveying is the process by which cartographers (map makers) calculate the distances and heights between pints before creating a map.
Because the terrain is often uneven, surveyors must find a way to take measurements of distance in a systematic way. The Pythagorean Theorem is used to calculate the steepness of slopes of hills and mountains. A surveyor looks through a telescope toward a measuring stick a fixed distance away, so the telescope’s line of sight and the measuring distance form a right triangle. Since the surveyor knows the distance of the stick from the telescope, he can use the theorem to find the length of the slope that covers the distance, and from that length. Determine how steep it is.
Painting on a wall
Painters use ladders to paint tall buildings and often do so with the help of the Pythagorean Theorem. The painter needs to determine how tall a ladder needs to be to safely place the base away from the wall so it will not tip over. In this case, the ladder will be the hypotenuse. Let us say a painter has to paint a wall that is 3m high. The painter has to place the base of the ladder 2m away from the wall to be sure it won’t tip over. You can calculate the length of the ladder using the Pythagorean Theorem. 32+22=h2 (hypotenuse, which is the length of the ladder). H=3.6m, so the length of the ladder needed is 3.6 meters.
As you see, mathematics is very important in our everyday life.